MÉTODO DE INTERPOLACIÓN
¿QUÉ ES?
La interpolación es un proceso para estuimar valores que quedan entre puntos de datos conocidos. La interpolación implica construir una funcion f cuyo valor sea el de unos valores de datos proporcionados y, en unos sitios de datos proporcionados x, de forma que f(x)=y, para todo i.
La interpolación f se construye normalmente como una función única de la forma

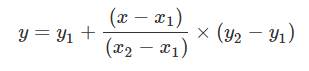

Comentarios
Publicar un comentario